Entretien avec Philippe Roux (15/11/2013)

Philippe est professeur agrégé de mathématiques à l'IUT de Lannion. Titulaire d'une thèse en mathématiques, il enseigne depuis 2001 les mathématiques appliquées aux étudiants du DUT d'informatique en utilisant Scilab (Retrouvez-le sur sa page personnelle).
Il est l'auteur du livre Scilab: De la théorie à la pratique - 1. Les fondamentaux.

Philippe, tu enseignes les mathématiques appliquées à l'IUT de Lannion, est-ce dans ce cadre que tu utilises le plus Scilab ?

Oui, c'est effectivement pour des raisons pédagogiques que je me suis mis à travailler avec Scilab. Au début des années 2000, j'ai commencé à enseigner en DUT informatique, les mathématiques occupent une place très importante dans cette formation. Le volume horaire de mathématiques y est important (250 à 300 heures sur deux ans, suivant les options choisies par les étudiants) et un programme qui touche à beaucoup de domaines : logique, algèbre linéaire, analyse numérique, probabilités, théorie des graphes, voire traitement du signal et imagerie numérique ! Mais l'enseignement des mathématiques devenait difficile face à des jeunes ayant choisi une formation permettant une insertion professionnelle rapide ET des poursuites d'études en école d'ingénieur. Pour intéresser ce public, il fallait trouver une synergie entre le côté académique des enseignements de mathématiques et les applications pratiques des notions utilisées en informatique. J'ai alors cherché un logiciel qui permette aux étudiants de passer par eux-mêmes d'une théorie mathématique à sa mise en pratique, Scilab s'est rapidement imposé à moi comme le bon outil : une syntaxe simple, très proche de celle utilisée en mathématiques, des boîtes à outils qui couvrent de nombreux domaines, une communauté d'utilisateurs/développeurs ouverte et active...   et en plus c'est un logiciel libre !

Mais l'utilisation de Scilab se limite-t-elle à l'enseignement ou y a-t-il d'autres domaines où tu apprécies l'aide de ce logiciel ?

En effet, Scilab est devenu pour moi un outil incontournable. L'utilisation quotidienne de Scilab à l'IUT de Lannion m'a permis de découvrir les nombreuses possibilités du logiciel qui n'est pas qu'un logiciel à but pédagogique, il s'agit d'un véritable environnement de prototypage qui permet de tester rapidement des algorithmes puis de développer une solution, en un temps court, solution qui pourra être convertie ou interfacée avec d'autres langages. 

"J'utilise en permanence Scilab
pour explorer différents domaines techniques
avec mon œil de mathématicien"

Pour cela, il existe toute une palette de boîtes à outils spécialement adaptées : depuis SIVP pour le traitement d'images à Xcos pour la simulation en passant par Metanet pour la théorie des graphes. Elles sont souvent créées par des développeurs externes mais travaillant en étroite collaboration avec l'équipe de Scilab Enterprises. J'utilise donc en permanence Scilab pour explorer différents domaines techniques avec mon œil de mathématicien. Parfois cela conduit à des idées que je pourrai réutiliser dans mes enseignements parfois c'est juste pour le plaisir !

Comme en astronomie ! Parle-nous un petit peu de cette passion que tu as... Comment l'apport de Scilab se concrétise-t-il ?

L'astronomie amateur est effectivement une de mes passions, c'est un domaine où se mêle à la fois des connaissances très théoriques comme la mécanique céleste, l'optique, la photométrie ... et des compétences très pratiques pour construire ou modifier des montages optiques, traiter des images obtenues avec une webcam ou un APN. Il y a donc une grande variété de sujets en astronomie, et pour chaque sujet on peut aborder les choses d'une manière théorique, en lisant des livres sur l'astronomie, ou par la pratique en observant le ciel... Pour moi, Scilab vient faire l'interface entre ces deux approches. En partant de modèles théoriques, on peut utiliser la puissance de calcul et les capacités graphiques de Scilab pour explorer et comprendre ce qui se passe pratiquement ! C'est ce que j'ai voulu montrer dans mon livre avec l'exemple de la simulation d'une orbite cométaire, mais avec le même outil, on pourra facilement simuler le fonctionnement optique d'un télescope ou effectuer du traitement d'images sur des clichés du ciel qu'on aura pris soi-même.

Tu veux dire que tu utilises Scilab pour retoucher tes clichés du ciel...?

Pas forcément. En effet, Scilab possède encore quelques limitations, en particulier au niveau de la mémoire disponible pour les calculs (limitation qui disparaîtra dans la prochaine mise à jour de Scilab 6) et les algorithmes de traitement d'images sont souvent très gourmands en mémoire ! Cependant Scilab permet d'implémenter assez facilement un algorithme demandant de nombreux calculs, il permet donc d'étudier en détail le fonctionnement d'un algorithme pour le comprendre ou l'améliorer avant de passer à une implémentation dans un autre langage (C++, Java, etc.), qui elle sera utilisée en production. C'est en cela que c'est un outil de prototypage qui peut être utile aux ingénieurs.

"Scilab permet d'implémenter assez facilement
un algorithme demandant de nombreux calculs"

Prenons l'exemple de la reconstruction d'une image : il arrive que la qualité d'une photo soit détériorée, par un bougé, de la buée ou un défaut de mise au point, et qu'on ne puisse pas la refaire. C'est un problème qui arrive souvent en astronomie quand on opère dans de mauvaises conditions. Dans ce cas, on a envie de pouvoir "réparer" les images obtenues lors d'une nuit d'observation sans recommencer tout le processus de prise de vue. C'est ce qui m'est arrivé, par exemple, en novembre 2007 : J'effectuais un suivi presque quotidien de la comète 17P/HOLMES qui connaissait un sursaut d'éclat particulièrement brutal. Un soir, j'ai réalisé une série de clichés en à peine une demi-heure, entre deux averses, et quand j'ai voulu traiter mes images je me suis rendu compte que la mise au point était plus qu'approximative. Dans l'impossibilité de refaire ces photos, j'ai alors cherché une méthode pour pouvoir les restaurer. Scilab m'a permis de tester les deux principaux algorithmes de déconvolution applicables dans ce genre de cas : le filtrage de Wiener et l'algorithme de Richardson-Lucy. Lors de mes tests sur des versions réduites des images, j'ai pu voir que l'algorithme de Richardson-Lucy donnait de meilleurs résultats. Je l'ai alors utilisé sur une version en pleine définition (avec le logiciel de traitement d'images astronomique Iris) pour obtenir une image nette de la comète montrant le jet principal et l'enveloppe circulaire en expansion.

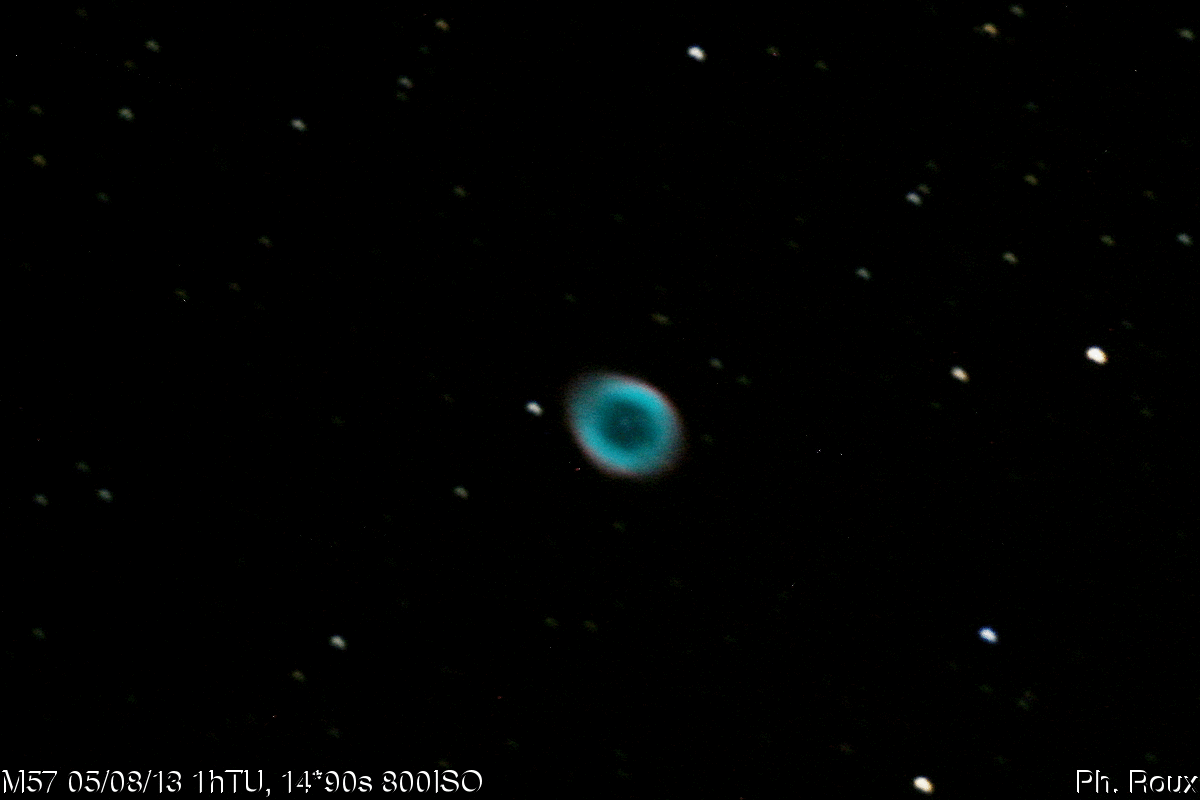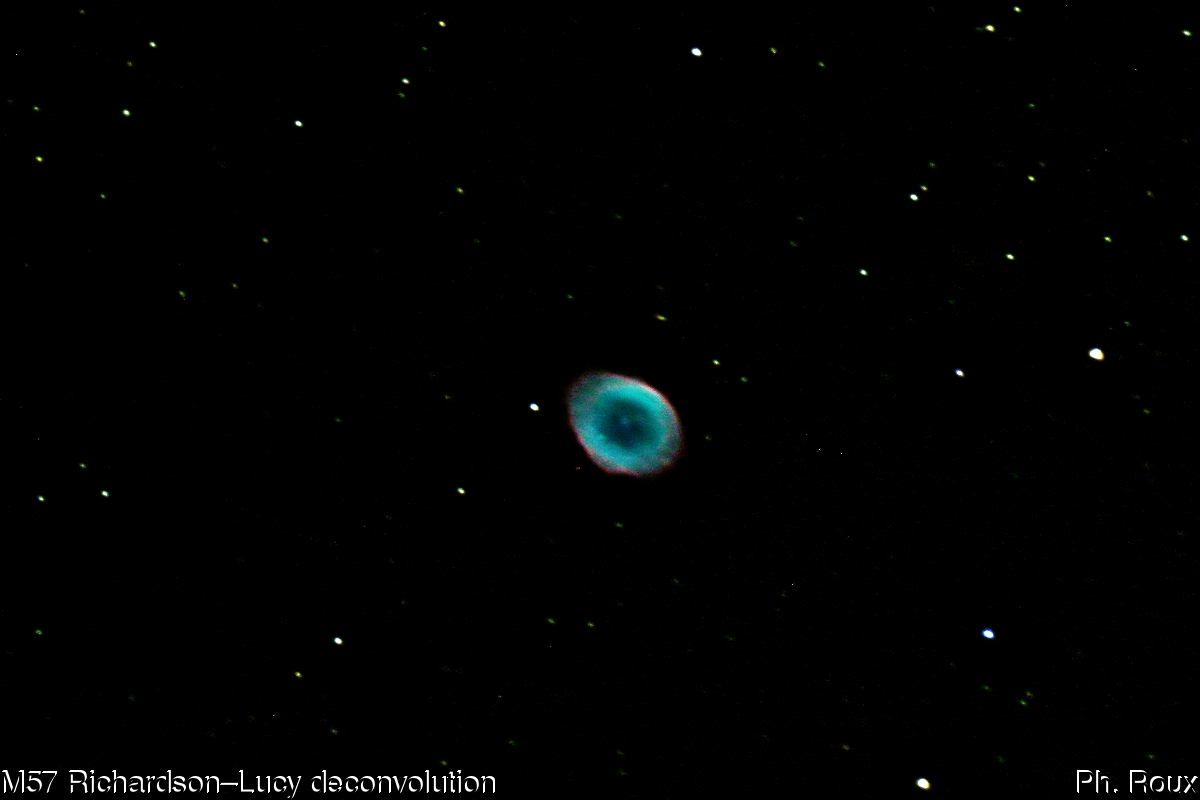
Un exemple de l'efficacité de l'algorithme de Richardson-Lucy

Pour comprendre l'utilité de faire des tests dans un cas comme celui-ci, il faut bien se rendre compte que le traitement final des images en pleine définition a demandé plus d'une heure de calcul et 2Go de mémoire sur ma machine ! Un outil comme Scilab permet donc d'étudier et comparer l'efficacité de divers algorithmes sans la lourdeur d'une implémentation faite à l'aide d'un langage compilé comme C++ ou Java.

 Pour conclure, et pour le plaisir des yeux et de l'esprit, j'aimerais encore que tu nous présentes une ou deux simulations animées obtenues avec Scilab...

C'est vrai j'aime beaucoup réaliser des animations graphiques à l'aide de Scilab, souvent dans un but pédagogique, car les capacités de Scilab dans ce domaine sont excellentes. Une animation est un moyen agréable et efficace de visualiser un processus complexe comme on en rencontre souvent en mathématiques.

"Une animation est un moyen agréable et efficace
de visualiser un processus complexe
comme on en rencontre souvent en mathématiques."

Par exemple, pour visualiser en trois dimensions des objets aussi étranges que le ruban de Moebius ou la bouteille de Klein, rien de mieux que de les tracer à l'aide de Scilab, puis de les observer sous toutes les coutures comme dans l'animation suivante :

Pour finir voici un dernier exemple lié à l'astronomie : je me suis récemment intéressé à la stabilité d'une solution du problème des trois corps découverte en 1993 par Cris Moore (voir son article Braids in Classical Dynamics). Cette solution est assez étrange puisqu'elle fait orbiter trois objets de même masse dans une ronde infinie en forme de 8.

Pour étudier la stabilité d'une telle orbite, on utilise les mêmes calculs que pour la simulation d'une orbite cométaire présentée dans mon livre en modifiant légèrement les paramètres de l'orbite. Si on modifie seulement de quelques pour cent les positions ou les vitesses initiales de ces trois objets alors la trajectoire d'ensemble des trois corps reste proche du "8" de départ, modulo une petite dérive à chaque orbite.

Par contre, si on modifie même très légèrement les masses des trois objets, le système devient chaotique conduisant probablement à la collision de deux des objets...

...ou à l'éjection du troisième.

La simulation de ce problème mathématiquement très complexe est à la portée de tout programmeur maîtrisant un logiciel comme Scilab.

Merci, Philippe, pour ces exemples, fort rêvants...